Understanding the core principles behind Within Visual Range (WVR) aerial combat is crucial for appreciating the skill and precision involved in dogfighting. This involves delving into Basic Fighter Maneuvers (BFM), the tactical movements fighter pilots execute to gain a positional advantage over an adversary. BFM are not arbitrary actions; they are deeply rooted in the fundamentals of aerodynamics, physics, kinematics, energy management, and geometric positioning. At their heart, these maneuvers combine aerodynamic flight principles and pursuit geometry with the critical physics of managing an aircraft’s energy-to-weight ratio, known as its specific energy. Mastering these Fighter Aircraft Maneuvers is fundamental to survival and success in close-quarters air combat.
Understanding Basic Fighter Maneuvers (BFM)
Basic Fighter Maneuvers (BFM) constitute the foundational skill set for pilots engaged in air combat maneuvering, or dogfighting. The primary goal is always to achieve a positional advantage relative to the opponent. This advantage might mean getting into a firing position, denying the opponent a firing opportunity, or forcing the adversary into a disadvantageous energy state. Executing BFM effectively requires a deep understanding of the aircraft’s capabilities and limitations across its entire flight envelope, particularly concerning its energy state and turn performance.
The Core Pillars: One-Circle vs. Two-Circle Fights
Since the dawn of aerial combat, dogfights have largely revolved around two fundamental concepts: the One-Circle Fight and the Two-Circle Fight. These remain cornerstones of modern air combat doctrine, even with advancements like Helmet Mounted Displays (HMDs) and Thrust Vectoring (TV). Pilots are rigorously trained in these concepts during their Introduction to Fighter Fundamentals (IFF) courses.
The One-Circle Fight: Winning the Radius Battle
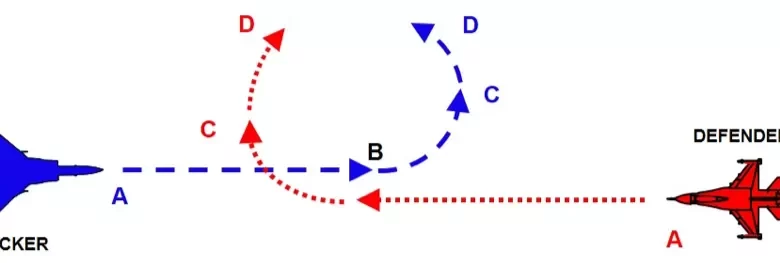
Also known as a “radius fight” or “nose-to-nose fight,” the one-circle engagement involves both aircraft maneuvering on essentially the same circle, often leading to their flight paths crossing.
Diagram illustrating the initial merge and turn in a one-circle fighter aircraft maneuver.
Imagine initiating a fight head-on (Point A in Fig. 1). The pilot intending a one-circle fight aims to leverage their aircraft’s superior turn radius against an opponent less capable in this regime. The typical game plan involves maneuvering vertically upwards upon merging. This climb reduces airspeed significantly, which, according to the physics principle where turn radius (r) is proportional to the square of velocity (V²), minimizes the aircraft’s turning circle.
Post-merge trajectory in a one-circle fight showing aircraft climbing to reduce turn radius.
Executing a climbing maneuver at the merge also reduces the aircraft’s forward movement vector, increasing the chance of maneuvering inside the opponent’s turn radius (post-merge, Fig. 2). Back in the cockpit, after the merge where the opponent (Red) passes your six o’clock, you initiate a sharp pull-up, keeping visual contact (“tally”). If Red turns left, you turn left (Point C). The essence of this fight becomes achieving the minimum turn radius faster than the opponent. As the engagement progresses (Points C-D), the aircraft often cross nose-to-nose in a “flat scissors” maneuver. The aircraft that first achieves the smallest radius and slowest forward speed gains the positional advantage, potentially securing a firing solution (Point E).
Let’s analyze this using an F-16 Turn Performance chart (Fig. 3), noting the chart’s A, B, C points differ from the maneuver diagrams.
To optimize for a radius fight, a pilot might aim for a merge speed around 430-450 Knots (Kts) / Mach 0.8 (Point A on the chart). At this point, the F-16 can achieve a turn radius of roughly 2,500 ft, a turn rate of 20 deg/sec, sustaining 9 Gs. Immediately post-merge, the pilot pulls Gs, often vertically, to bleed speed towards approximately 300 Kts / Mach 0.6. This targets Point B on the chart, representing the minimum achievable turn radius (around 2,000 ft), tangent to the aircraft’s flight envelope limit. At Point B, the turn rate is about 18 deg/sec. However, this state is often instantaneous. To maintain a near-minimum radius, the pilot might follow the blue line towards lower speeds, accepting a reduced turn rate. At Point C (around 150 Kts / Mach 0.3), the turn radius remains minimal (below 2,000 ft) with a 10 deg/sec rate, intersecting the “SEP=0” (Specific Excess Power = Zero) curve. This signifies the aircraft can maintain speed and altitude in the turn without needing extra power – a highly efficient state for a radius fight. Successfully reaching and maneuvering near these points represents optimal exploitation of the aircraft’s capabilities in a one-circle scenario.
The Two-Circle Fight: Dominating the Rate Battle
Alternatively known as a “rate fight” or “nose-to-tail fight,” this engagement involves the aircraft maneuvering on two distinct, albeit interacting, circles.
Diagram showing pre-merge setup for a two-circle fighter aircraft maneuver.
Entering the merge (Fig. 4), if your aircraft possesses a superior turn rate compared to the opponent, a two-circle fight is advantageous. The objective here is not the smallest radius, but the highest sustainable turn rate.
Post-merge spiral descent in a two-circle fight aiming for maximum turn rate.
Looking again at the F-16 performance chart (Fig. 3, Point A), the highest instantaneous turn rate (20 deg/sec) occurs around 430-450 Kts / Mach 0.8 and 9 Gs. The key challenge in a rate fight is maintaining a speed close to this optimum throughout the engagement. Since pulling 9 Gs at this speed results in negative SEP (SEP < 0), the aircraft loses energy rapidly if solely relying on engine power. Therefore, pilots typically initiate the post-merge maneuver by rolling and pulling the lift vector below the horizon (Fig. 5), entering a descending spiral. This trades altitude for speed (potential energy for kinetic energy), helping to maintain the high airspeed needed for the optimal turn rate.
This type of high-G, descending maneuver is physically demanding. Pilots must maintain visual contact by looking back towards the opponent while pulling maximum Gs, often without referencing instruments. Pilot G-tolerance becomes a critical factor; the pilot who can sustain the high G-load longer often prevails.
However, the maximum instantaneous rate (Point A, 20 deg/sec) is fleeting. As energy bleeds off, maintaining this rate becomes impossible. Pilots must then transition towards a sustainable condition.
F-16 turn performance chart emphasizing sustained speed (SEP=0) in a two-circle rate fight.
Referencing the second F-16 chart, after the initial high-G pull, the goal shifts. Once altitude available for trade is depleted (reaching the “combat floor”), the pilot aims to maintain speed within the “sustained speed” range. This is typically where the flight envelope allows maneuvering along the SEP=0 line (Point B on this chart). For the F-16, this occurs roughly between Mach 0.65 and 0.75. In this range, the aircraft can sustain a turn rate of about 14 deg/sec at around 6 Gs without losing energy (speed or altitude). Fighting at sustained speed allows the pilot to continue maneuvering effectively without rapidly depleting the aircraft’s energy state.
Beyond the Merge: Dynamic Combat and Pilot Skill
While understanding one-circle (radius) and two-circle (rate) Fighter Aircraft Maneuvers is fundamental, real-world dogfights are far more complex and dynamic. Engagements rarely remain purely one type. Pilots continuously assess the situation, transitioning between radius and rate strategies based on relative positioning, energy states, and opponent actions. The first minute of an engagement is often frantic, involving high-G pulls and rapid energy changes. Subsequently, the fight might settle into a more sustained maneuvering phase. Ultimately, victory in a dogfight isn’t guaranteed by flying the technologically superior aircraft. It often belongs to the pilot who better understands both their own and the enemy’s aircraft performance, who can more quickly place their jet at its optimal performance point for the given situation, and who skillfully adapts their tactics throughout the fluid, high-stakes environment of aerial combat. The ability to execute the right fighter aircraft maneuvers at the right time remains paramount.
