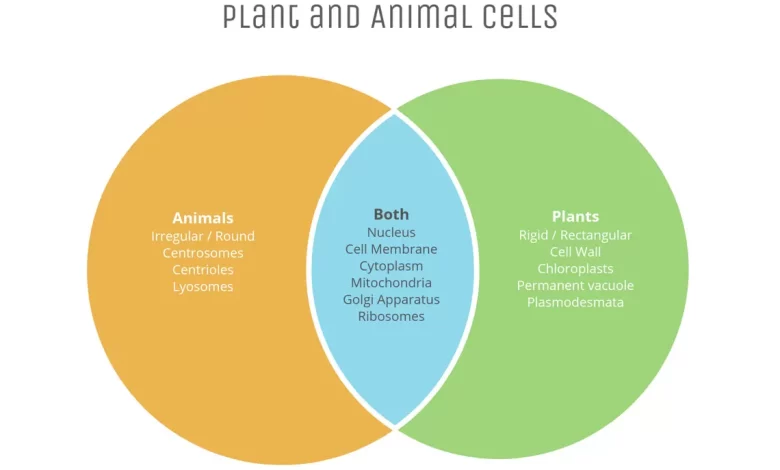
A Venn diagram, also known as a set or logic diagram, serves as a powerful visual tool to illustrate the differences, similarities, and overlapping relationships between distinct sets or groups of data. One of its most common applications is to clearly depict shared characteristics between otherwise different entities. A prime example that helps clarify its function is using a Venn Diagram Of Plant And Animal Cells to show what features they have in common and what makes them unique.
Venn diagram showing the differences and similarities of plant and animal cells
In a Venn diagram, a data set is represented visually as a collection of points enclosed within a boundary, typically circles (though ellipses or other shapes can be used). Each circle represents one category or set, containing all the data points that share a common characteristic defined by that set. For instance, in the diagram comparing animal and plant cells, one circle encompasses characteristics specific to animal cells, such as irregular/round shape, presence of centrosomes, centrioles, and lysosomes, while also including common organelles like the nucleus, cell membrane, cytoplasm, mitochondria, Golgi apparatus, and ribosomes.
The key feature of a Venn diagram is the intersection—the area where the boundaries of two or more sets overlap. This overlapping region visualizes the data points or characteristics that are shared by all the intersecting sets. In the context of the Venn Diagram Of Plant And Animal Cells, the central overlapping area clearly indicates the organelles and features present in both types of cells. While Venn diagrams can involve multiple intersections and circle sets, the most frequently encountered is the three-circle, or triple, Venn diagram.
A noteworthy aspect of the triple Venn diagram is the creation of a central curved triangle shape, known as the Reuleaux triangle. This shape possesses a constant width and has captivated professionals across various fields, including engineers, mathematicians, architects, and graphic designers, due to both its mathematical properties and aesthetic appeal. It has been utilized by notable figures like Franz Reuleaux for kinetic mechanisms and Leonardo Da Vinci for map projection.
Triple Venn diagram with central Reuleaux triangle
The Evolution and History of the Venn Diagram
The concept behind Venn diagrams, abstract visual representations of conjunctions and intersections, is ancient, with similar visual tools appearing as early as the Middle Ages. The fundamental human desire to categorize and show relationships between groups has led to the organic development and refinement of such logical diagrams over centuries.
Gottfried Wilhelm Leibniz, a German polymath and philosopher in the late 1600s, is one of the earliest figures directly associated with this style of diagrammatic representation. Leibniz championed the use of symbolic visualization for complex ideas, believing it improved communication and reduced the potential for errors and disagreements inherent in purely verbal or written explanations. He saw formalized logic diagrams as a means to visualize and calculate differences of opinion.
The Contribution of Euler Diagrams
Roughly a century after Leibniz, the renowned Swiss mathematician Leonard Euler gained recognition for his use of overlapping circles to represent logical conclusions or syllogistic reasoning. Euler diagrams are used to depict the four fundamental categorical propositions of syllogism:
- The Universal Affirmative (e.g., “All mammals are animals.”)
- The Universal Negative (e.g., “No fish are birds.”)
- The Particular Affirmative (e.g., “Some students are artists.”)
- The Particular Negative (e.g., “Some cars are not electric.”)
Euler diagram illustrating a universal affirmative syllogism
Euler diagram showing two disjoint sets with no overlap
Euler diagram depicting a set as a subset of another
Euler diagram showing partial overlap between two sets
In contemporary data visualization practice, it has become common to loosely group both Euler and Venn diagrams under the more widely known name “Venn diagram” to simplify terminology and minimize confusion. A distinction between the two is usually only critical in more technical mathematical or logical contexts.
The Modern Venn Diagram
The specific type of diagram we commonly refer to as a Venn diagram today was formally introduced by the English mathematician John Venn. In 1880, he published a paper titled “On the diagrammatic and mechanical representation of propositions and reasonings.” In this work, Venn proposed an evolution of Euler diagrams to serve as a more comprehensive visualization tool, particularly for probability, by requiring that all possible logical outcomes or intersections be represented, even if they contain no data. The term “Venn diagram” itself was coined later, in 1918, by American philosopher Clarence Irving Lewis.
Since Venn’s publication, the diagrams have been the subject of extensive research by many other notable scientists, including A.W.F. Edwards, Branko Grunbaum, and Henry John Stephen Smith. They have become a fundamental visualization in mathematical study, used not only in the traditional 2- or 3-circle forms but also in more complex versions incorporating spheres and ellipses. These diagrams are essential in fields such as set theory, logic theory, the study of rotational symmetry, and the exploration of complex mathematical objects like the tesseract. Understanding the basic representation, such as the venn diagram of plant and animal cells, provides a gateway to grasping these more advanced concepts.
What is NOT a Venn Diagram?
Despite their straightforward appearance, Venn diagrams are often confused with or mislabeled, most frequently being mistaken for Euler diagrams. While all Venn diagrams are indeed a type of Euler diagram, the reverse is not true.
The key difference lies in the representation of possibilities. A Venn diagram must visualize all possible logical intersections between the sets, even if some intersections are empty (contain no data). An Euler diagram, conversely, visualizes only the relationships and intersections for which data actually exists. The provided [venn diagram plant animal cells](https://shocknaue.com/venn-diagram-plant-animal-cells/) example implicitly follows the Venn principle by showing distinct areas for Plant Only, Animal Only, and Both.
Consider the following diagram, which is a typical Euler diagram illustrating the relationship between Venn diagrams and Euler diagrams:
Euler diagram illustrating that Venn diagrams are a subset of Euler diagrams
This diagram accurately shows that the set of “Venn Diagrams” is entirely contained within the set of “Euler Diagrams,” meaning every Venn diagram is an Euler diagram. However, the Euler diagram set is larger, indicating there are Euler diagrams that are not Venn diagrams. If this were forced into a strict Venn diagram format, it would have to show a theoretical intersection of “Euler Diagrams that are NOT Venn Diagrams” alongside the “Venn Diagrams (which are also Euler Diagrams)”, implying a possibility that doesn’t exist mathematically (a Venn diagram that isn’t an Euler diagram).
Let’s illustrate the difference with a practical example involving three friends, Lucy, Anwar, and Jans, and their homework assignments. Lucy completed two assignments: “Prokaryotes & Eukaryotes” for Science and “Probability & Statistics” for Math. Anwar did his Math homework on “Probability & Statistics” but chose “Animal Cells & Plant Cells” for Science. Jans wrote an essay on “Mitosis & Meiosis” for Science but failed to do his Math homework.
We can visualize this information using both diagram types:
Euler diagram representing student homework completion and topics
The Euler diagram above shows only the actual completed homework. It correctly depicts the overlap where Anwar and Lucy both did their Math homework on the same topic. Since Jans’ work didn’t overlap with the others in topic or completion, his circle remains separate.
Now, let’s see the same scenario as a Venn diagram:
Venn diagram representing all possible outcomes for student homework completion and topics
This Venn diagram shows the same completed homework information, but it also includes empty intersections representing possibilities that could have occurred logically, even if they didn’t in this instance. For example, the intersection between Jans and Anwar’s circles (excluding Lucy) represents the possibility that Jans and Anwar completed Math homework on the same topic, but Lucy did not. The central intersection represents the possibility that all three friends completed their Math homework on the same topic. The structure mandates the representation of all potential overlaps, regardless of actual data. This is also relevant when studying specific biological comparisons; an [animal cell and plant cell worksheet answer key](https://shocknaue.com/animal-cell-and-plant-cell-worksheet-answer-key/) for a Venn diagram exercise would require understanding these distinct regions representing ‘only plant’, ‘only animal’, and ‘both’.
Furthermore, a diagram that lacks any commonality between sets also doesn’t qualify as a Venn diagram. If two data sets share absolutely no characteristics, their circles would not overlap at all, forming disjoint sets. While this is a valid Euler diagram, it’s not a Venn diagram.
Diagram showing two separated sets with no common elements
Conversely, if two data sets are identical, the Venn diagram would simply appear as a single circle, as the boundaries would completely overlap.
Even some diagrams that show multiple intersections are not mathematically complete Venn diagrams. For instance, a diagram with four circles arranged such that not all possible pairwise or group intersections are represented (e.g., an intersection exists only between sets A and B, but not theoretically possible for A and C) does not meet the criteria of a true Venn diagram.
Diagram of four intersecting circles that is not a mathematically complete Venn diagram
This four-circle arrangement, while visually appealing, fails the test of a Venn diagram because it does not depict every possible logical intersection (e.g., there is no region representing the intersection of only the yellow and the red circles, or only the blue and the orange).
Summary
In conclusion, a Venn diagram is:
- A specific type of Euler diagram.
- A visualization tool using two or more overlapping circumferences (typically circles) to represent sets of data.
- Used to clearly show the differences, shared commonalities, and relationships between these data sets.
- Characterized by its requirement to depict all possible logical intersections between the sets, even if some intersections are empty.
- An incredibly useful tool for comparison across various fields, from mathematics and logic to biology, as seen in the common example of the venn diagram of plant and animal cells.
